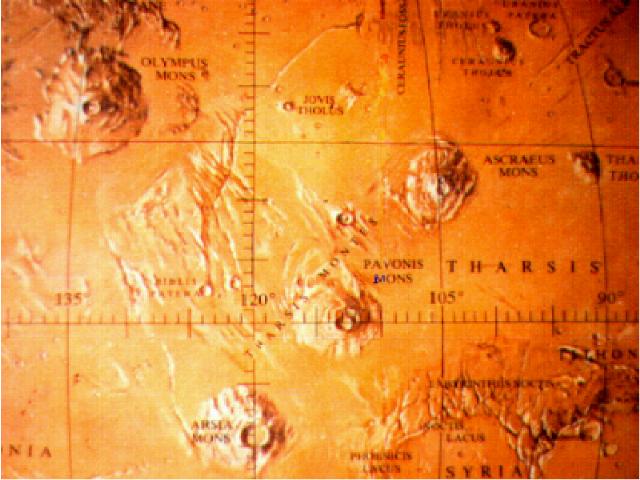
A kürtõk
átmérõje 60-120 km. A vulkáni dóm átmérõje
400-500 km-es.
|
Piramisok
Szerzõ: Földes Attila |
| Ma
már az nem kérdés, hogy valaha vol-e élet a
Marson.
A kérdés: Milyen formába léteztek,és mi történt velük. A következõ állításaim feltételezések az üzenetküldõkrõl. El tudjuk olvasni az üzenetüket, de értetlenül állunk felette. Vajon miért ilyen formában küldték? Valószínû, hogy biológiájuk eltér a miénktõl. A vulkán-rendszer magas intelligenciát mutat a Marson, de az teljesen eltérõ technikájú és kultúrûjú, mint a miénk. Például a vulkánok létrehozása. Fel kell tételezni, hogy más biológiájuk volt, mert használták a Tang-Lang nyelvet. Agyuk 'huzalozása' teljesen eltérhet a miénktõl. Lehet, hogy szemük olyan érzékeny, hogy í mértani szög látásakor azonnal érzékelik a szög tangensét 8 tizedesig. Így õk egy másik világot látnsk. Az üzenet ezt sugallja. A szemük lehet, hogy alapvetõen eltér a miénktõl. Mi kimondtu, hogy más intelligenciák lehetnek, de ha találkozunk vele nem fogadjuk el. A szemük valószínûleg sokkal érzékenyebb, mint a miénk. Szemük foveája hasomló lehet mint a miénk csak 10 000 szer nagyobb és érzékenyebb. Talán egyszerre látják a számok rengetegét, és a feladatnak legmegfelelõbbet azonnal ki tudják választani. Ez lehet az oka, hogy számunkra elképzelhetetlen kapcsolatokat tudnak bemutatni.(Pl. Radián szög, Nap-Föld, Nap-Mars távolság, a valós Nap-Föld távolság kicsinyített távolsága, mindez egyetlen háromszögbe sûrítve). Például a Nap-Föld távolság esetén a 149 530 000 km-t 'beállítja' az agyában, akkor megjelennek ehhez a számhoz kapcsolódó minden variáció. Például ez is: 149 530 000 = 702 x 21283 x 10 Nap-Föld = 702 x Mars kerület x 10 Ez a módszer
hasonlít az internet mûködéséhez, csak
sokkal gyorsabb lehet. Nem kívánok most szólni a kollektív
gondolkodásról, mert nagyon vad következtetésekre
jutnánk.
|
1./ A vulkán-rendszer, mely bizonyos matematikai-geometriai, kozmoszi állandókat, eljárásokat mutat be.
2./ A dombok (50-60 m-es dombocskák a Marson) közötti kapcsolatrendszer, melyet Profs. Horace Crater fedezett fel. Mondhatjuk az ajtó feltárult, de a szobába még nem léptünk be.
3./ A piramisok, a dombok és a fej funkciói.
A Mars Északi fékgömbjének kéregvastagsága nagyon csekély. Itt vulkánt indítani nem nehéz. A kéreg évmilliárdos zártsága biztosítja, hogy a vulkánok helyben maradjanak. Lehet, hogy a Mars légköre vulkáfûtésû volt ?
 |
Ezek
a hatalmas vulkánok.
A kürtõk
átmérõje 60-120 km. A vulkáni dóm átmérõje
400-500 km-es.
|
| 2Pi Radián = egy teljes kör = 360° = 21283 km |
| 1./
Az elsõ 3 jegy mindig pontos. Példáué a Mars
kerülete 21 283 km. Ez a szám a megadott
pontossági rendszerben: 21200 km. 2./ Minden állítást legalább 3 más-más módon meg kell ismételni. 3./
Meg kell mutatni a szerkesztések módszerét, de nem
az egész szerkesztést. Azt fel kell
|
 |
A két
'szem' közötti vonal nagyon fontos. Ez képez kapcsolatot
a vulkánok, a 'fej' és a piramisok között
A vulkán-rendszernek
két 'szeme' van. Ezeket összekötöttem egy vonallal.
Nézzük
meg milyen kapcsolata van a 'fej'-el. Megtalálható vajon
a piramisoknál is?
|
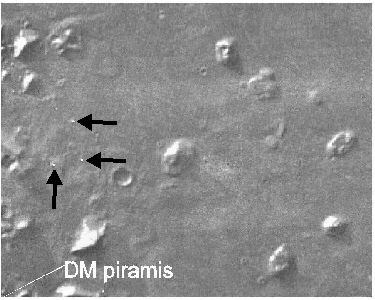 |
A Nap ilyen
szögállásában jól látható
a 'fej'.
De más szögállásokban el is tûnhet. Ezt a tudósok is tudják. Ha megtudnánk, hogy az arc (fej), miért pont ott van, ahol van, talán valamivel többet elõbbre haladnánk. Mindenesetre próbáljuk meg. A kép felsõ-bal, és alsó-bal sarkában van egy-egy hatalmas piramis. Milyen eredményre vezetne, ha itt is alkalmaznánk a vulkán-rendszer módszereit ? Nézzük elõször alul a rekonstruált DM piramist. (alul) |
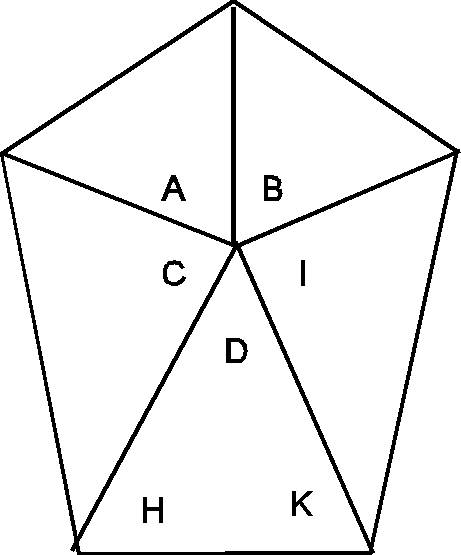 |
A DM piramist
tanulmányozta és jól értékelhetõvé
tette Profs. Dr. James F. Strangle. A piramist meteor becspódás
érte, ezért rekonstruálta.
A szögeit tanulmányozta. Ez látható a rajzon. Mindenek elõtt nézzünk egy példát. Négyzetgyök 3=1,7320 Ez 60°-os szögnek felel meg, mert Tg(60°) = 1,7320 Ezt az eljárást ismerjük a Tang-Lang fejezetbõl. Nézzük ez a módszer alkalmazható-e itt is? |
| J.F.Strangle
szögei
Tang-Lang nyelven
-------------------------------------------------------------------------------------- A = 60° Tg(60°) = gyök(3) B = 60° Tg(60°) = gyök(3) C = 85.3° Tg( 85.45 ) = 4xPi=12.56..... D = 69.4° Tg( 69.80 ) = 'e' = 2.718.... H = 55.3° H = 55.1° K = 55.3° K = 55.1° H+K=110.6° tg(55.1+55.1) = -2.718 = -'e' I = 85.3° I = 84.75° Tg(84.75°)=10.88292144 2Pi=tg(84.75°)/sqrt(3))=6.2832576223 (11 decimal punctuality!!) (2Pi Radián egy teljes kör) ----------------------------------------------------------------------------------------- 60+60+85.3+69.4+85.3 = 360 60+60+85.45+69.80+84.75 = 360 ----------------------------------------------------------------------------------------- Hihetetlen és csodálatos. A Tang-Lang nyelven megszólal a piramis !! Mit is mond nekünk ? gyök3....., gyök3....., 4xPi....., 'e'......, '-e'......, 2xPi...... Ezek mind állandók és a kozmosz minden pontján ugyanannyi. Mint láthatjuk ugyanazt a módszert alkalmazták, mint a vulkáni rendszernél is. De a DM piramis titkainak megismeréséhez elõbb meg kellett ismerni a vulkán rendszert. (Csak zárójelben. A kis 'e' a mérnökök kedvenc száma. Nagyon sûrûn használják a magasabb számításoknál. Úgy nevezik: A természetes logaritmus alapszáma). A piramis nem szimmetrikus. Csúcsa a fej felé irányított. Egy jól irányzott nyil a fej irányában. A félmilló km-rõl már látható vulkán rendszer ismerete nélkül a finomabb, kisebb objektumok közötti összefüggéseket sohasem fedeztük volna fel. Az bizonyosnak tûnik, hogy a Marson legalább 3 intelligencia fejlõdött ki. Ezek tudtak egymásról. Most pedig nézzük meg hogyan kombinálták össze a Mars kerületét a piramisokkal és a 'fej'-el. A valós Nap-Föld távolság: 149 530 000 km. Õk ezt lekicsinyítették a Mars felületére. A kicsinyítés mérõszáma 702,6 x 21 283 x 10 Itt a 702,6 km a második fejezetben tárgyaltak szerint egy kimetszett távolság, 21283 km pedig a Mars kerülete. 149 530 000 = 702,6 x 21 283 x 10
|
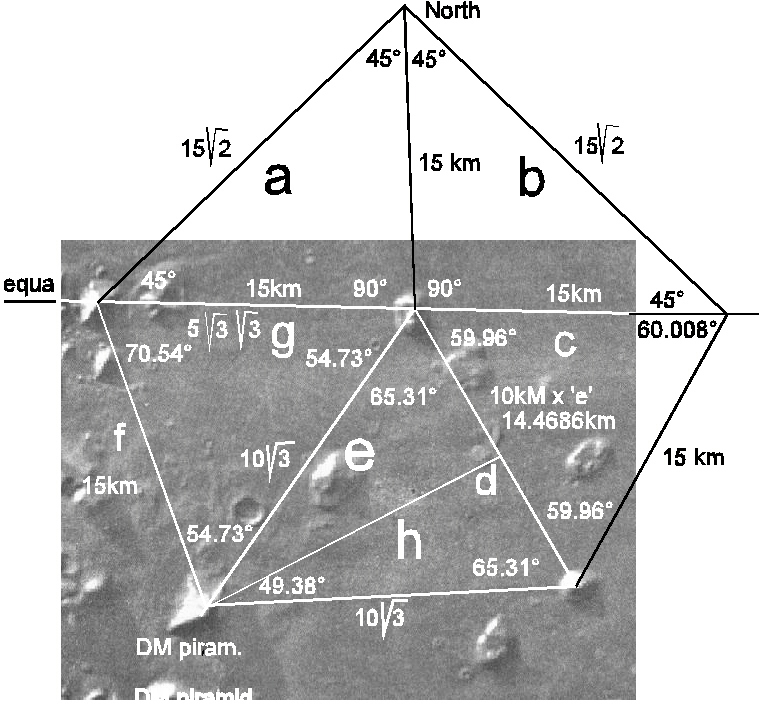
Amikor felismertem ezt a hatalmas ötszöget rögtön a vulkán rendszer jutott eszembe. Keresni kezdtem a két szemet összekötõ egyenest. Az egyenes egy hatalmas piramis csúcsához vezet. ( 'g' vonal). A térképemet ezután kalibráltam, hogy mérni lehessen a távolságokat. A 'g' vonalat 15 km-nek mértem. A két piramis közötti távolságot szintén 15 km-nek találtam. Megmértem a jobb szem sarkát és a DM piramis csúcsának távolságát. Ez 17,32 km-nek adódott. Nem lehetett pontosabban mérni. De lássunk csodát. 10 x gyök(3) = 17,3205 km !! Tekintsünk
vissza a törvényünkre. Azt mondja: Az elsõ
3 jegy mindig pontos. Ez azért van így, mert 3 számjegynél
(osztásnál) pontosabban nem tudunk mérni. Ez cm, mm,
tized mm. Az én térképemen ez 10 méteres pontosságot
mutat.
Ezzel azt is bizonyítják, hogy az üzenet a Földnek szól. Megpróbáltam
alkalmazni valahogyan ezt a szem-kis hegy 'd' távolságra.
Nézük
ezután az Attila ötszöget. Lásd a következõ
rajzot.
Itt megálltam.
Nem találtam semmi fogódzót a továbblépéshez.
Menjünk hát vissza a vulkán-rendszerhez.
|
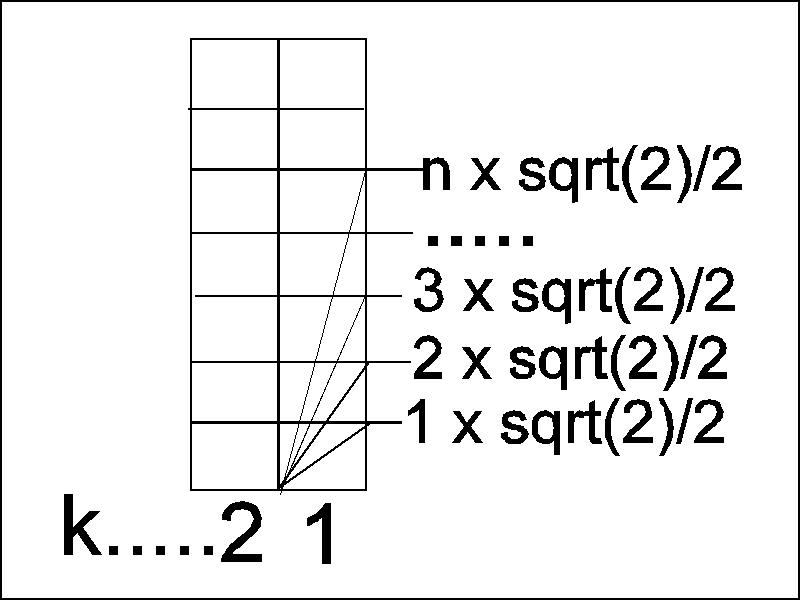 |
A
számított szögek:
Arctg(nxgyök(2)) / 2) n=1, 2, 3,.. n A leghosszabb oldal: gyök(k**2)+(A**2) Ez esetben k=1 |
************************************************************************************************************
Ellenõrizzük
az eredményeket.
A
fenti táblázatnak csak a 'C' oszlopát nézzük.
Mit találunk?
gyök(3),
és a 2,345 szám. Ne feledjük hogyan készítettek
derékszögû háromszöget az egyiptomiak.
Vettek
egy kötelet. Készítenek rajta egy csomót. A végétõl
számítva ez lesz az 1 egység.
Most
4 szer rámérik ezt az egységet és ott is készítenek
egy csomót, majd folytatva 5ször felmérik és
ott is készítenek egy csomót. Ha kötél
végét és A 3 cdomót kifeszítjük,
akkor egy pontos derékszögû háromszöget kapunk.
Ez
azért van mert 3, 4, 5: (3**2)+(4**2)=(5**2)=9+16=25
Érdekes
felfedezni, hogy a 'C' oszlopban megtalálhatóak a 3, 4, 5
számjegyek.
A 'D' oszlopban
felfedezhetjük a ritmusosságot. 0,707 = 1 x gyök(2)/2,
2 x gyök(2)/2.......
Megtaláljuk
a 2,12, 21,1 számokat, melyek a 21 283 km-re utalnak, melyek
a nagy ötszög 15xgyök(2)-ben is megtalálható.
A 3 számjegy
pontosságot tartva. Ha teljesen pontos adatot szeretnénk,
úgy a távolságot század milliméter pontossággal,
15,05 cm-re kellene mérnünk. Ekkor 15,05 x gyök(2)=21,283
amely pontosan a Mars kerületének számai.
A 212 számok
feltûnnek az n=3 és n=30 esetén. Ha k=2, k=3...k=n
eseteit is megvizsgálnánk lehet, hogy érdekességeket
találnánk. A rácsozat még nincs befejezve.
A
végsõ megoldás a küldõ intelligencia gondolkodásmódjának
megismerése.
Összefoglaló::
| DM piramis | AP (Attila-ötszög) | Dombok és Rács | |
| 1 | O (arány) | ||
| sqrt(2) | OO (távolság) | O... (ratio) | |
| sqrt(3) | O (ratio) | OOO (distance) | O... (ratio) |
| sqrt(5) | O (ratio) | ||
| 'e' | O (ratio) | ||
| -'e' | O (ratio) | ||
| 4Pi, 2Pi | O (ratio) O(ratio) | ||
| 19.47° | OOO | ||
| kerület | O O (distance) | OO (ratio) | |
| kMars egység | O (distance) | ||
| egyenlítõ | O (distance) | ||
| 345 oldalú háromszög | O | ||
| Nap-Vénus/Nap-Merkur | OO (ratio) |
A dombok további tulajdonságai.
| Lehet,
hogy mindez csak a természet játéka . De mi történne
akkor, ha valaki a természet véletlenjeit összgyûjti,
rendszerezi és így adja közre. Ekkor már nem
véletlen a véletlenek halmaza.
I'm
waiting for your opinion.
|