Before we deal with the tang-Lang of cosmos let we recognise the earth's tangent ABC.
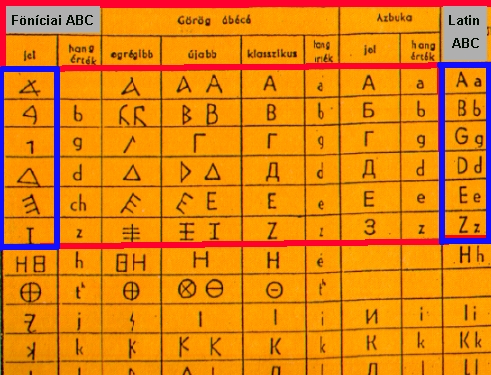
The ancient phoenicians used this letters. Only the first 6 letter existed in the most ancien times.
So, A,  B,  G,  D,  E,  Z.
                                                                        greek
                                  Phoenician   ancient    newer   classic

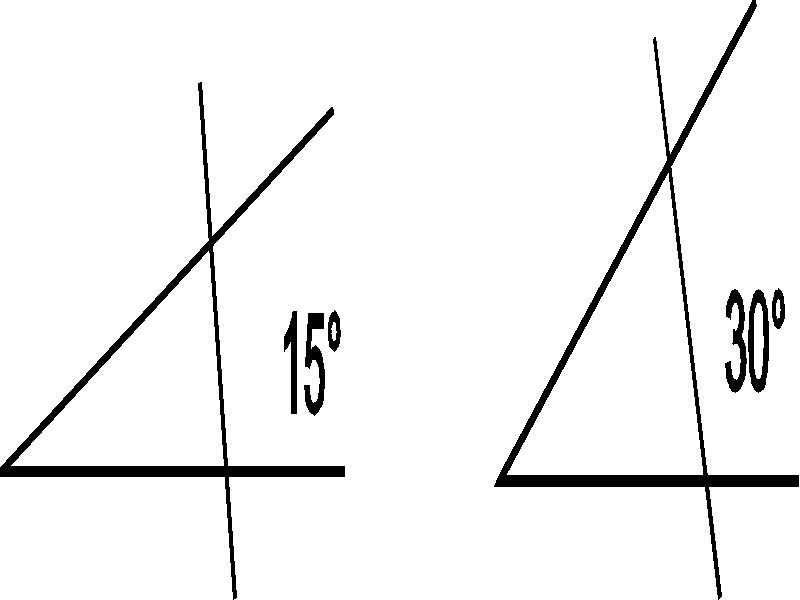
Even like this we could be mistaken, if we were to be just a little careless in how we drew the sign. What is to be done ? The two angles could be distinguished by depicting the angle with a curved marking, denoting that the angle were bigger. If the curve were well-defined it certainly  would  not be misinterpreted.

           A                   B
 
          15°            15+15=30°

When the Phoenicians began to work out humanity's first letters they “stole” our idea, so to speak, since in the last phase of the procedure explained above it was the Phoenicians letters “A” and “B” that we designed.
 Now let us continue following the system of letters that proceeds  in steps of 15 degrees.
The next step is to 45 degrees.
           G
  45°  This is the most ancient phoenician G.
      30+15=45

The Phoenician “G”, today's Greek and Cyrillic “G”.
 What is the next one ?
Letter “D”, which according to its place in the order corresponds to an angle of 60 degrees, since
45 +15 = 60
  60°    The Phoenician “D” is delta in today's Greek alphabet.
D =45+15=60
 

 But let us hurry on. The next one is 60 +15=75 degrees. At this stage we run out of ideas, for not one mathematics textbook enlarges upon how to obtain the mathematical value of this angle. It is complicated! Let us consider that we already have 45 degrees and 15 degrees. If we draw the 45 degrees, we can add to 15 degrees “beards” : 45+15+15= 75.
       E    This became our letter “E” of today.
  45+15+15=75°
 

 The 90 degree angle presents no problem, because this has to show the end of the procedure. That is, the 90 degrees.
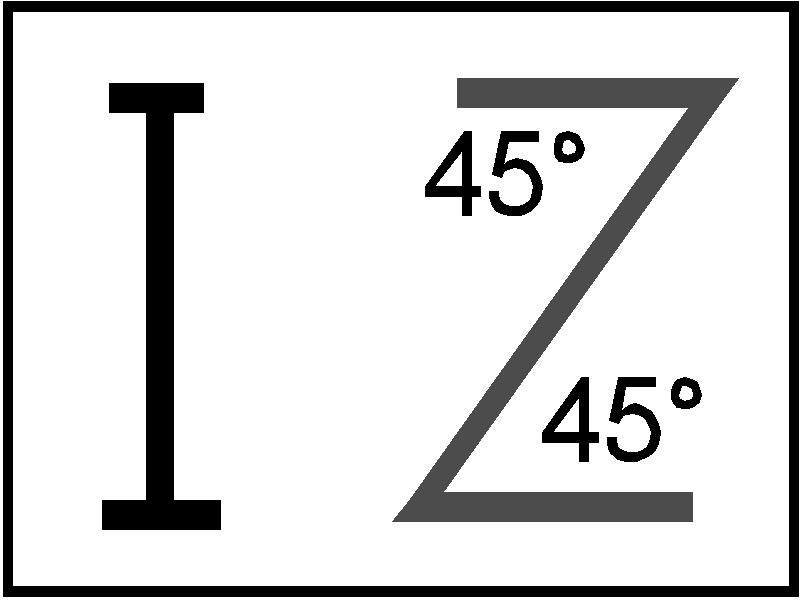.         This letter “Z” today, and always has been.
             45+45=90°

  We must go no further, for we have reached the ancient letter denoting the end,  “Z”. Thus from our ancestors we inherited 5 valid letters and a symbol representing the ultimate letter.
 The  first 5 letters are the PENTATONIC  symbols.
 
 Now, let we see some explains from the volcan-system message.
 

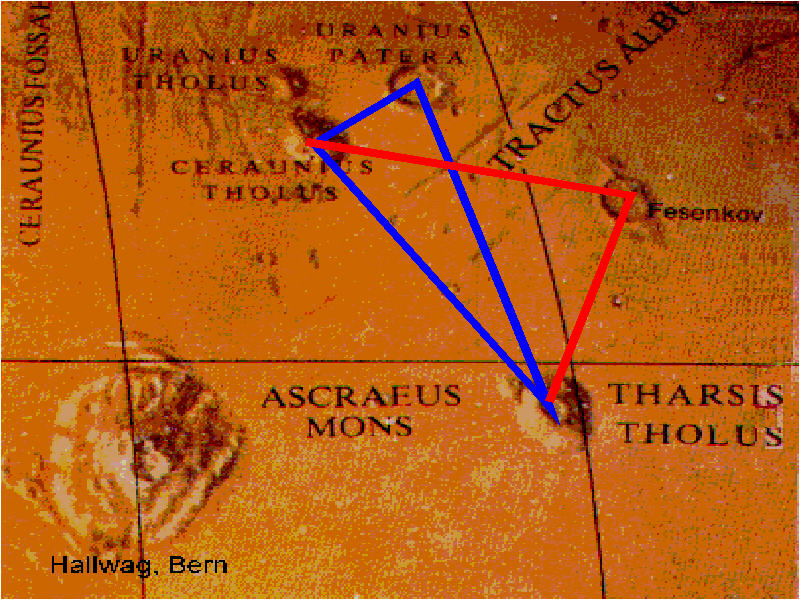Fig. 2.          Between the eyes is a basic line for two triangles.      We will look at this.      (Map, Hallwag, Bern)

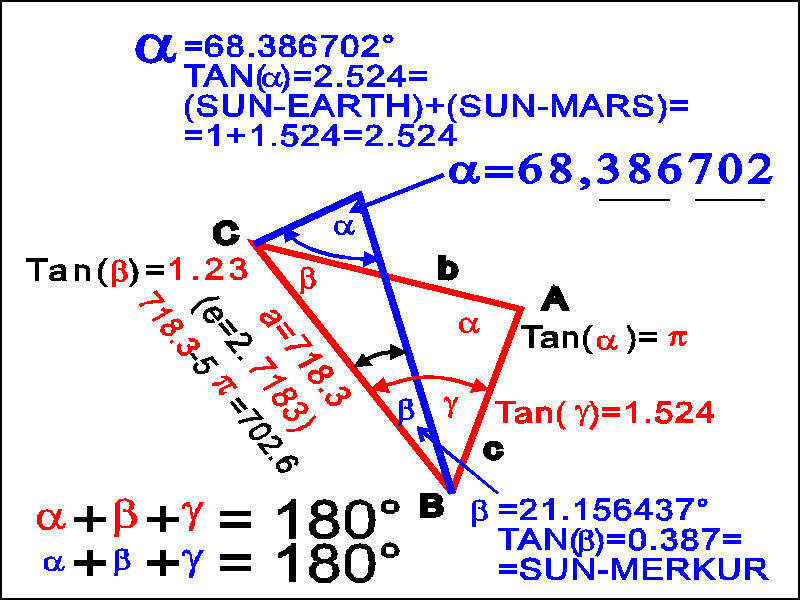Fig. 3

The use of “Tangent construction”. 

Let we verify them.

All astronomical data is repeated in “tangent language”.
Datas of the red triangle:
                  alfa   =72.343213°         (Tg (a) = Pi )         ( The Pi )
                 beta   =50.92839°          (Tg (b) = 1.23)       ( range of the numbers )
                 gama =56.728397°        (Tg (g) = 1.524)     ( The Sun-Mars distance)
               ————————
                            180.000000 °

Datas of the blue triangle:

alfa       = 68.386702°             (Tg(alfa) = 2.524 = Sun-Earth (1) + Sun-Mars(1.524))
beta     = 21.156437°              (Tg(beta) = 0.387 = Sun-Mercury
gama   = 90.456861°
 

Look at the crater above the upper eye, slightly to the right. (See fig. 3). This appears to be the result of some meteorite crashing down, because an enormous flat area  surrounded by a great ditch has been produced. (Directed meteorit?). And still, it is a volcanic area, for tests show it to be a hotspot. From the centre of this hotspot the rim of the volcanic crater is traced out like an arc.
 It  is not a mound, a dome that is in question here, but a level area surrounded by a ditch. If we were to use our hands to mark out a direction radiating from the centre, then the rim of the crater  would trace out the arc in exactly the same way as at school we used a compass to mark off points between two lines.
 The astronomical data given so far is repeated  in yet another way.
 Now, possessed of the knowledge of the tangent, let us return to our level crater.
 Notice the small triangle marked in blue, seen above the eyes. The tangent value of our angles give the same number as was seen on the diagram shown  earlier. That is, 2.524.  This is the sum of the values Sun-Earth=1 and Sun-Mars=1.524. (1+1.524=2.524).(See fig. 2, fig. 3)
 Only, here it is not a straight line that has been divided into such a ratio, but it is the sides of a triangle that are the different distances. Which is why an angle also appears in the ratios of the sides. This  angle  represents the value of 2.524 as the tangent of the angle.
 A justifiable question can be raised,  namely what  angle (alfa) has the tangent of 2.524 ? The answer is 68.386... degrees, because tan(68.386702)=2.524. This is the Tangent-Language. It is known by anybody but not used. The other angle of the triangle also carries important information. It shows the Sun-Mercury  mean distance. (0.387), because  tan(21.156437)=0.387.
 But here, likewise, attention must be given to the decimals, for they could be important.
 Just as the angle of the 1773.6 km angle sides repeated the 1773.6 in angle 50.61773 degrees, putting the decimal 6 to the front, so in the decimals here 0.387 and 702.6 are joined up and appear as 68.386702 degrees, which is now the fifth expression of the astronomical base unit. (Later the middle distance of Mercury can be seen).
 Now we can understand why the mean distances of Earth and Mars had to be dealt with as the sum of two values. (1+1.524=2.524).
 This is the only way in which, with one angle, we can express:

 - the Sun-Earth astronomical unit ........................................(1.00 AU),
 - the Sun-Mars astronomical distance  ................................(1.524 AU),
 - the Sun-Mercury astronomical distance ............................(0.387 AU),
 - the reduced value’s digits of the astronomical distance     (0.007026).

 This seems unbelievable. It seems that the geometrical order of these formations  wishes to teach us something, just as Frendenthal tried with his alphabet to teach the extraterrestrial intelligences.
 Naturally, the truth of the angles might be doubted, since exact measurements could not be made, due to the distortion caused by the “spherical view” given. In Fact, this system could only be proven as true if it were to turn up in places where the truth contained in it could be defined with greater accurancy.
 Which is why the single triangle found previously is not proof enough. What would be really satisfactory is if, where called for, this data were to appear again, but this time in the form of the above “tangent-language”.
 Let us see if this is so.

 To the north of the lower  Mars-crater of the large triangle there are  two small volcanic craters.
 Since, likewise, we are on the equator we can carry out our measurements with no great complications, because the angles and the distances will be relatively accurate. The only inaccurancy will be found in the difference there is between the lines of latitude and longitude.
 The small volcano, once again, is of a peculiar form, but let us not bother with that for the time being.
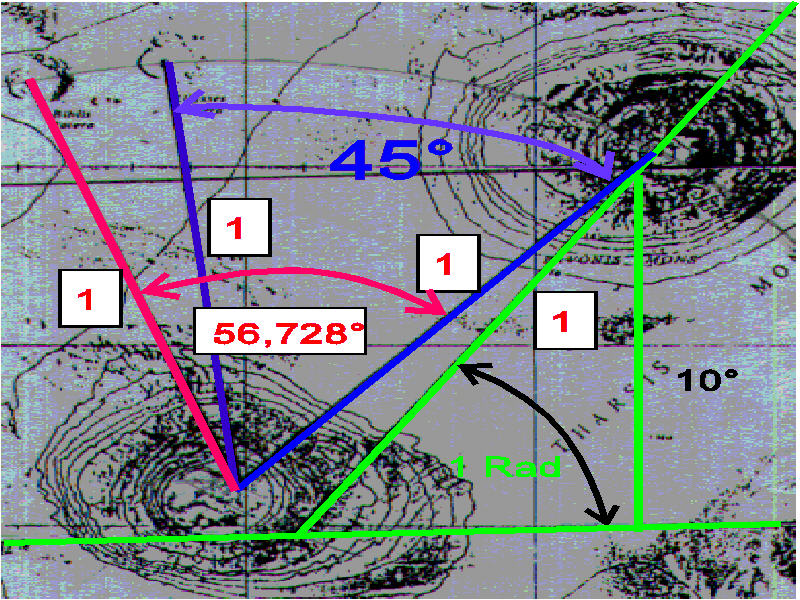
 Of the two little volcanoes, one is nearer to the Earth volcano, the other to Mars. Let us look at the angles first. We will examine the one near to the Earth volcano. Its angle of inclination is exactly 45 degrees. The tangent of this is 1, that is, it represents the Sun-Earth distance (1). This is no suprise, it is exactly where it ought to be.
 The other - the one close to Mars - is at 56.73 degrees. It is not possible to measure this with such accuracy, but now we know exactly  the value it should be.
   

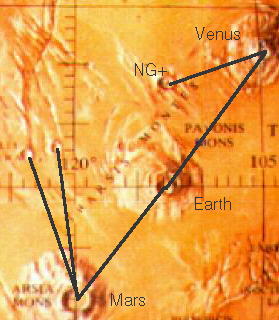
Fig. 4

.
The green, the blue and the red distances are equal long. It is computed by the 10° and 1 radian. The blue and red angles are 45° and 56.728°. This well measured by anybody. 

Let use the Tang-Lang language: 
Tang(45°)=1 and this is the Sun-earth middle distance. Blue angle.

Tang(56.729)=1.524
This is the sun-earth middle distance. Red angle.

 It should correspond to the value of the angle whose tangent gives 1.524 for here it is right next to the Mars crater. At last the 1 and the 1.524 can be found in a different form, nicely divided, to show that the addition of the number was deliberate, and this serves to  lessen our doubts.
 The two small craters are at equal distances from the big Mars crater. That is to say, the two small craters are connected by their data.
 But let us look at the area around Venus, too. We can find near left hand a small crate named Ng objekt by NASA.

 We find the astronomical datas again,  exactly where it ought to be, given in exactly the angle we would have expected. It should be noted that this small crater is at a distance that divides the Venus-Earth distance in two, giving a ratio of the Sun-Earth and the Sun-Mars distances e Sun-Mars distances (1 ans 1.524), and so, this is the foth method of conveying the data of Earth and of Mars.

 But let us take a look at the distances.

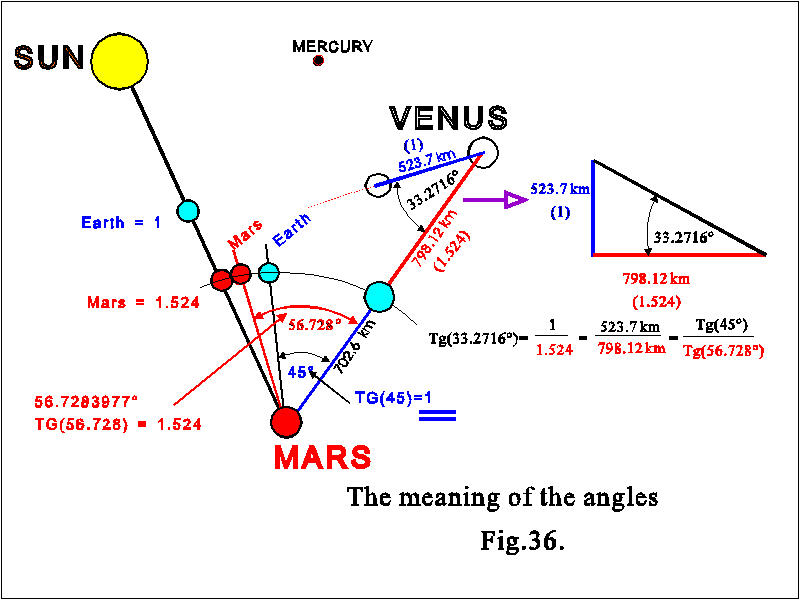
The distance between the Venus and Earth volcanoes is 798.12 km. ( upper volcanoe). If this represents the Sun-Mars distance - 1.524 -, then the distance of the Venus-Ng objective should be 798.12/1.524 = 523.7, which it is. Now 523.7 is one unit (Sun-Earth) and 1.524 times this (798.12 km) is equivalent to the Sun-Mars unit. If we measure the angle between the two distances we find that it is approximately 33.27 degrees. We are given the value exactly if we divide 523.7 km by 798.12 km or 1:1.524 =  0.6561679. This then, would be the tangent of the angle. Let us calculate the angle from this. Arctangent(0.6561679) = 33.27160(...). Such a presentation of the side lengths and the angles calls us to position the sides in a right-angle and in this interpretation we see the circular function of the tangent about which we learnt at school.
 
 

All rigths by Attila Foldes