|
Hangváltók II.
Hangváltók II. |
Nagyvonalakban az első részben átfutottuk a szűrők létjogosultságát és hatástalanítottunk néhány taposóaknát. Most megnézzük, hogyan tudjuk mindezt realizálni.
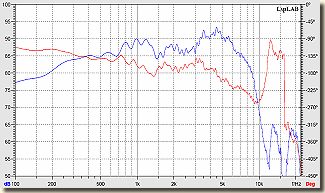
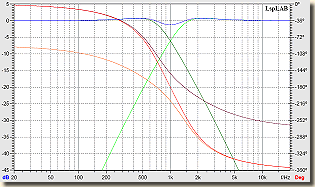
Az, hogy a szűrőknek van némi gondja a különböző görbékkel, azt már körüljártuk, de hogy maguknak a sugárzóknak is vannak hasonló gyermekbetegségei, az annyira már nem köztudott, pedig vannak. Az átviteli jelleggöbék fázismenete és amplitúdómenete között közvetlen összefüggés áll fenn: az amplitúdó jelleggörbe csúcs- és mélypontjai a fázis-jelleggörbe elkanyarodásában nyilvánulnak meg és ez fordítva is fennáll. Az amplitúdó 6 dB/oktáv változása például 90° fáziseltolódást eredményez, egy 12 dB/oktáv változás pedig 180°-ot, 18 dB/oktáv 270°-ot és 24 dB/oktáv 360°-ot. A különböző típusú szűrőknél a keresztezési frekvencia nem mindig jelenti azt, hogy az aluláteresztő és felüláteresztő szűrő határfrekvenciája az egy és ugyanaz, hogy mennyire húzzák széjjel, vagy összébb a görbéket, az attól is függ, hogy mekkora lenne a keresztezési frekvencián a kiemelés, vagy a csillapítás. Minden típusnál létezik egy un. kritikus csillapítású verzió, ahol a határfrekvenciák megegyeznek a keresztezési frekvenciával. A mellékelt ábra kék görbéje egy mély-közép sugárzó amplitúdó jelleggörbéje, a piros pedig a hozzátartozó fázismenet. Sajnos ezek azok az adatok, amiket a gyártók nemigen kötnek az orrunkra, maximum, a jobbaknál kapunk egy amplitúdó és impedancia görbét, valamint a T/S paramétereket táblázatban. Az ábrán megfigyelhető görbék egy valós, létező sugárzó mérőmikrofonos mérésének eredményei és ha jobban megszemléljük, elég érdekes következtetéseket vonhatunk le belőle. Nevezetesen, hogy a fázismenete kb. 110°-tól indul és bizony lemegy majdnem 270°-ig, legalább is ami az ábrán látható és mindezt abban a tartományban teszi, ahol használni szeretnénk. A rezonancia pontja 60 Hz környékén van, így a fázismenet 0 pontja kb. 30 Hz-nél lesz. Azon azonban erősen elfilózhatunk, a kék görbét nézegetve, hogy vajon melyik tartomány lesugárzására használhatnánk és mettől meddig. Azt hiszem, hogy az eddigiekből a napnál is világosabban kiderült, hogy nem elegendő venni 3 hangszórót, egy nagyot mélynek, egy közepeset középre és egy csipogót a magasaknak, aztán gyorsan összeütünk valamilyen keresztváltót és az egészet belelapátoljuk egy csinos dobozba. Na nem azt mondom, hogy ez nem fog szólni, fog, csak hogyan ?
Ergo, a kiindulási pont, a sugárzók beválogatása, mert hát azért lehet a fentebb látható görbéktől szebbeket is találni. A következő kérdés, hogy hány utasra is tervezzük a váltót és az a váltó millen is légyen ? Egy csipogó átfogási tartománya nagy általánosságban 1 kHz-től 20-30-40 kHz-ig terjedhet, egy spéci mélysugárzó, amelyik hajlandó levánszorogni 20 Hz környékére, az bizony már nem hajlandó 1 kHz-nél csicseregni, jóval korábban abbahagyja, amelyik elmegy idáig, az hálából az alsó regisztereket nem hajlandó megkörnyékezni. Tehát vagy belenyugszunk, hogy Hádészt nem fogjuk felidegesíteni és megússzuk egy kétutas váltóval, vagy beletuszkolunk hiánypótlásként egy harmadik sugárzót is középre és akkor már rögtön három utas váltót gyárthatunk hozzá. Ha netán túl nagy tartomány lesugárzását akarnánk rábízni egy mélysugárzóra, akkor számolnunk kell egy nem túl szimpatikus jelenséggel, a Doppler-torzítással. Ha a sugárzó membránja egyidejűleg rezeg mély és magas frekvenciákon, ekkor az alacsony frekvencia megmodulálja a magasakat, ami szintén az eredeti hangképben nem szereplő frekvenciák megjelenéséhez vezet, ami, mint tudjuk, nemlineáris torzítás. Megvan tehát, hogy hány utas lesz a rendszerünk, ezzel az is, hogy hány utas váltó kell hozzá, no de hol váltsunk ? No akkor üssük fel Murphy törvénykönyvét, mert ha még nem jeleztem volna, nem azon a frekin fogunk váltani, ahol mi szeretnénk, hanem bizony ott, ahol a sugárzók hagyják magukat. Ha van akkora szerencsénk, hogy a mély sugárzó ott hagyja abba a dudorászást, ahol a csipogó elkezdi, akkor nyilvánvaló a keresztezési frekvencia helye, de ha van kellően nagy átfedett tartomány, akkor kellő segítséget jelenthet a két sugárzó egymásra vetített fázismenete. A kellően kis fázishiba érdekében célszerű odatenni a keresztezési pontot, ahol a fázisgörbék egymást metszik, vagy legalább is, a környékére. Természetesen, ehhez rendelkeznünk kell az alkalmazott sugárzók amplitúdó és fázis görbéivel, és ha lehet, akkor az impedancia menetről se árt, ha van egy görbénk, amikhez vagy hozzájutunk a gyártótól, vagy megmérjük őket. Az impedancia görbe majd ott jelent segítséget, amikor már megtaláltuk a leendő keresztezési frekvenciát és bekéne pötyögni a Java-scriptbe az adatokat. Vizsgáljuk meg, hogy a sugárzók a váltási frekin mekkora impedanciával bírnak, ezt jó közelítéssel le tudjuk olvasni a görbéről és ezeket az értékeket írjuk be, ugyanis ekkor követjük el a legkisebb hibát a méretezésnél.
No akkor csapjunk a lecsóba ! Vegyük először a kétutas váltókat, amiből lehetséges soros ill. párhuzamos elrendezésű változat és hogy egyszerűbb legyen, mellékelek mindegyikhez némi számítási segédletet. A két impedancia és a keresztezési frekvencia ismeretében megkapjuk az alkotóelemek értékeit, de ha csak az utóbbiakat ismerjük, megkaphatjuk a váltó frekijét az Inverz-gomb használatával, már ahol van ilyen. A Java-scriptekben minden esetben a szűrők eredeti polinomjait használtam.
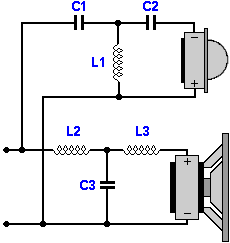
6 dB/9 dB/12 dB/oktávos soros keresztváltó
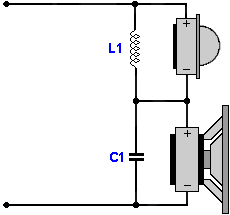
Ennek a váltótípusnak van egy rendkívüli jó tulajdonsága, némi polinom bizerálás segítségével, 9 ill. 12 dB/oktávossá is varázsolható.
6 dB/oktávos párhuzamos keresztváltó
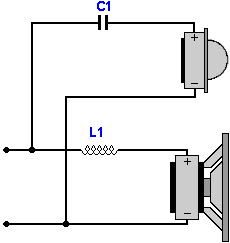
Sugárzók azonos polaritással bekötve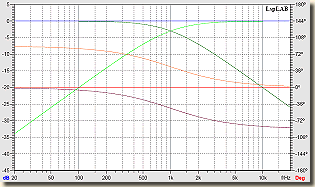 |
Magassugárzó ellentétes polaritással bekötve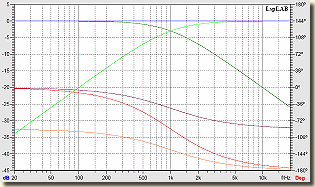 |
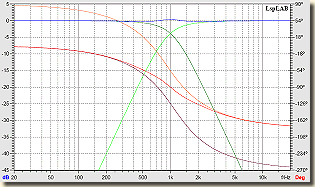
A kék görbe a sötétzöld aluláteresztő és a világoszöld felüláteresztő szűrő amplitúdómenetének az összege, a két fázismenet összege a piros görbe, a lila az aluláteresztő, a narancssárga a felüláteresztő szűrőé. Azt hiszem, elég világosan látszik, hogy az összegzett amplitúdó és fázismenet abszolúte lineáris és egyenes.
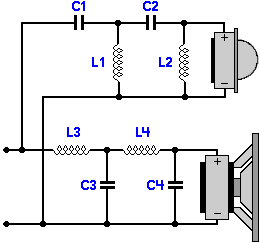
12 dB/oktávos párhuzamos keresztváltó
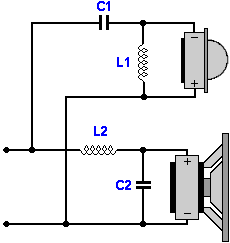
Sugárzók azonos polaritással bekötve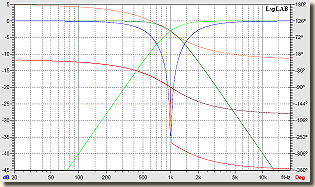 Butterworth szűrő 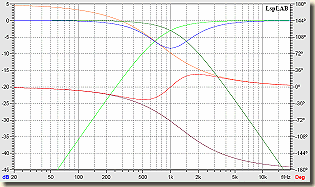 Bessel szűrő |
Magassugárzó ellentétes polaritással bekötve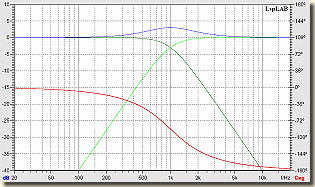 Butterworth szűrő 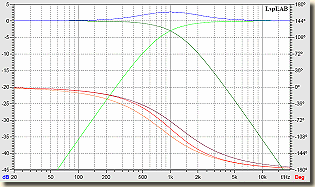 Bessel szűrő |
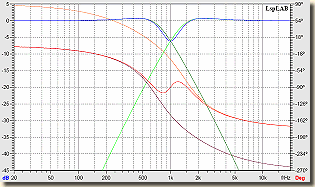
Az ábrákat szemlélve, talán világos, hogy miért is jelöltem a rajzon eleve fordított polaritással a csipogót. A +3 dB-es kiemeléssel és a konstans 180°-os fázistolással vagy megbarátkozunk, vagy ragozhatjuk a kérdést. Bár a Bessel-nek, azonos polaritású sugárzók esetén, ugyanolyan a fázismenete, viszont az a +3 dB-s hupli kissé lankásabb lesz. Ennél a szűrőtípusnál a Linkwitz-Riley féle adja az optimális megoldást az amplitúdómenetre, kiemelés nincs, a fázismenetet sajnos ez sem tudja optimalizálni.
18 dB/oktávos párhuzamos keresztváltó
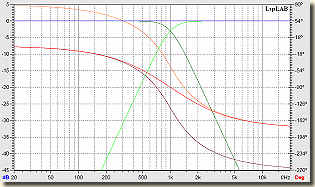
Elég hepe-hupásak ezek a görbék, az mindenesetre igen érdekes, hogy azonos polaritású sugárzók esetében a Butterworth szűrő eredő fázismenet átfogása bizony 360°. A 3.rendű váltók esetében a fázis linearizált Paynter-típusú, ill. a kritikus csillapítású a nyerő megoldás.
24 dB/oktávos párhuzamos keresztváltó
Sugárzók azonos polaritással bekötve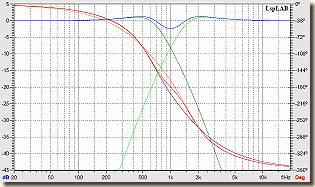 Butterworth szűrő 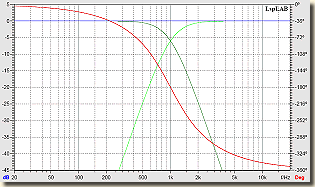 Linkwitz-Riley szűrő |
Magassugárzó ellentétes polaritással bekötve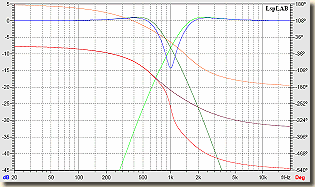 Butterworth szűrő 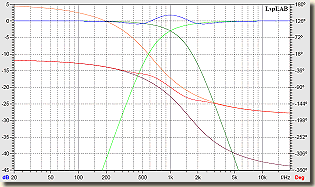 Bessel szűrő |
Ennél a szűrő típusnál egyértelmű, hogy amplitúdó szempontból a Linkwitz-Riley, fázis szempontból a Bessel a jó megoldás.
48 dB/oktávos párhuzamos keresztváltó
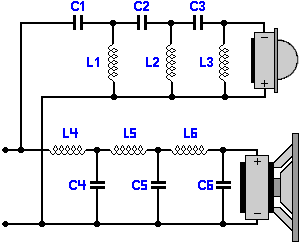
No, ez már csak a B-verzió és a perverzió kedvéért, de ekkora fokszámú szűrőt passzívba ritkán használnak.
folytatjuk
![]()