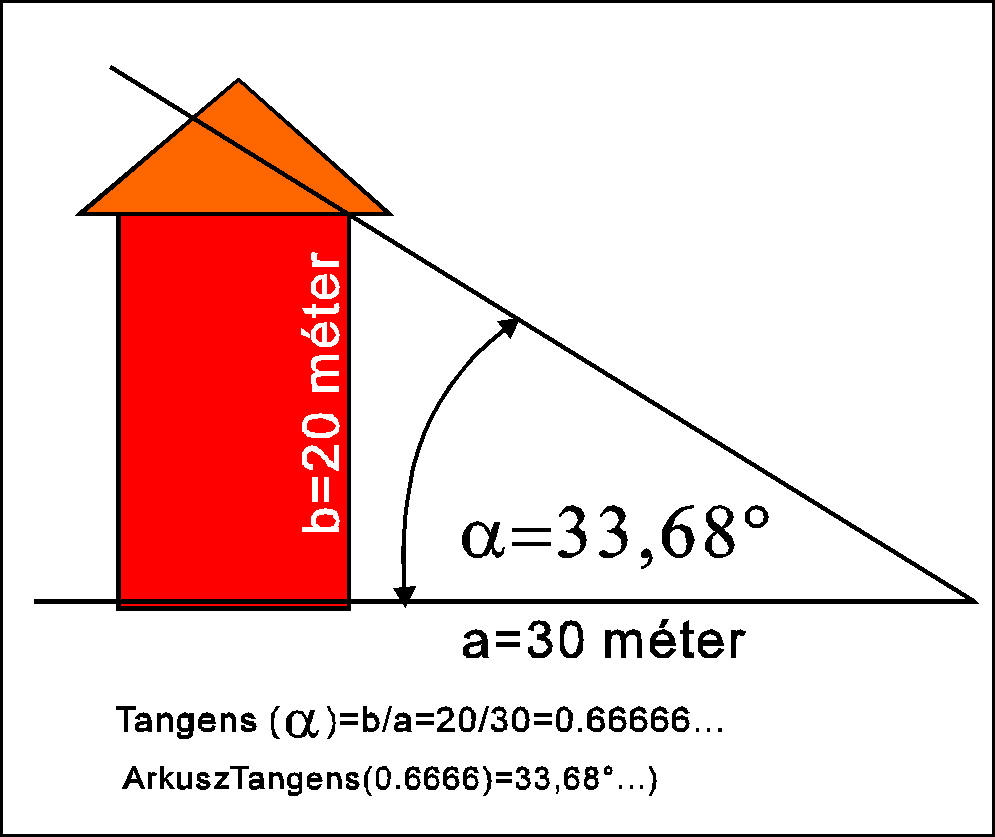
A Tangens szögfüggvény a kozmosz minden pontján ugyanazt az eredményt adja.

Mégis, ha átgondoljuk gyorsan belátjuk a "tang-lang" nyelv  értelmezésének korlátait.
Például: ha egy objektumot számokkal akarok jellemezni, akkor vagy két távolság arányát, vagy egy szöget meg kell adni.
Mielõtt foglalkoznánk a tang-lang kozmoszi ABC nyelvvel, nézzünk körül saját házunktáján, hátha itt a Földön is megtaláljuk.
Alább láthatjuk az emberiség elsõ betûírását, a föníciai írást. (Az ezt megelõzõ írások (Sumer, Akkád, stb. képírás, vagy szótag írás volt). Az Õsi föníciai írás elsõ 6 betûje eredendõ 6 betûbõl állt. A többit ezekbõl képezték, fejleszették ki.

Ez az elsõ 6 betû: A,  B,  G,  D,  E,  Z.  Vizsgálatunk az ábra kék keretes betûire vonatkozik.

                                                                 g ö r ö g
                                  Föniciai       legõsibb   újabb     klasszikus

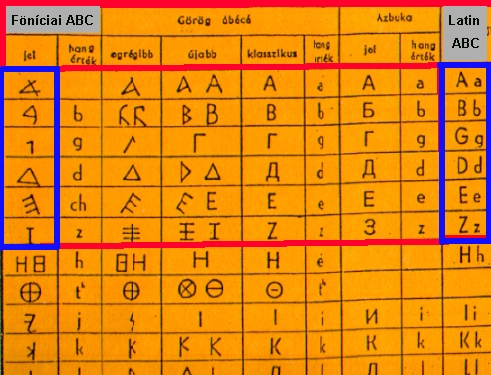Az Õsi föniciai ABC ezt mutatja.
 

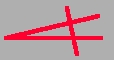
A               B                G            D                E              Z       15°            30°             45°          60°             75°           90°                                                                 45+15+15=75° 45+45=90°

A-tól  Z-ig, 15°-ként halad.
Az egyes betûknek olyanoknak kell lenniök, hogy olvasva könnyen meg lehessen különböztetni. Ezért az elsõ betûtõl  (A betût) a második betûtõl (B-tõl) meg kell különböztetni. Ecélból egy görbe ivvel ábrázolták a B betût. Igy az "A" betût (15°), és a "B" betût (30°) nem lehet összetéveszteni. Teljesen érthetetlen, de mégis azt látjuk, hogy az emberiség elsõ ABC-je 15 fokonkénti betûábrázolást mutat. Hihetelen, mert ez a kozmoszi tang-lang nyelv lényege. Minden számnak képe van és fordítva, minden képhez szám tartozik.
Feltétlenül meg kell jegyezni, hogy a 90°-os Z betû ma is használatos végjel. Ha ez a jel egy szótag  végét jelöli, akkor 5 jel (A-B-G-D-E) marad. Ez a pentaton skála 5 jegye. Mintha az õsõk a mondanivalót énekelve mondták volna el, és az 5 betû 5 hangérték lenne, vagyis 5 hangjegy.
Érdekes a zsidó írás, amelynél a betûk számokat is jelentenek.
Nézzünk ezek után pár példát a Tang-Lang nyelv marsi használatáról.
 

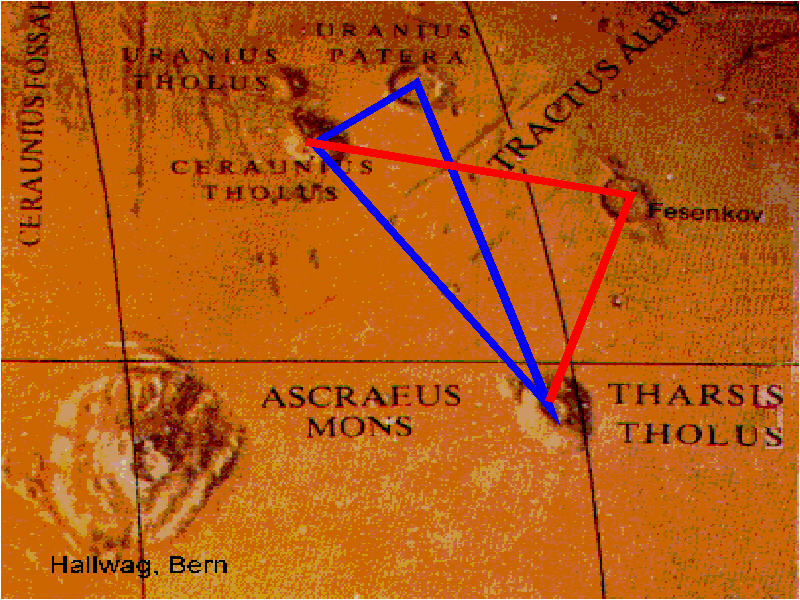Fig. 2.          Két háromszöget látunk, közös bázis oldallal. Vizsgálni fogjuk a háromszögek szögeinek értékeit.        (Map, Hallwag, Bern)

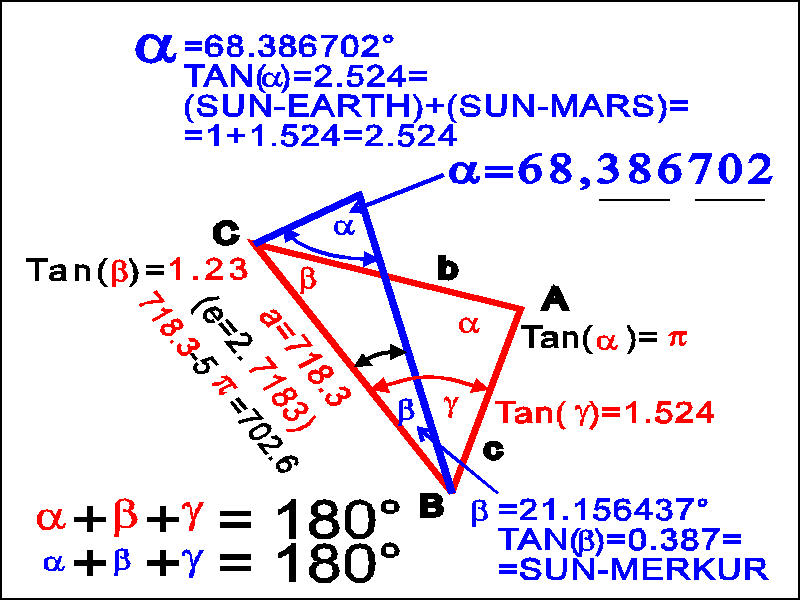Fig. 3

Ellenõrizzük, igaz-e?.

Minden csillagászati adatot megismételnek tangens nyelven is.
A piros háromszög adatai:
                  alfa   =72.343213°         (Tg (a) = Pi )         ( The Pi =3.14........)
                 beta   =50.92839°          (Tg (b) = 1.23)       ( range of the numbers )
                 gama =56.728397°        (Tg (g) = 1.524)     ( The Sun-Mars distance)
               ————————
                           180.000000 °
 

A kék háromszög adatai:
alfa       = 68.386702°             (Tg(alfa) = 2.524 = Sun-Earth (1) + Sun-Mars(1.524))
beta     = 21.156437°              (Tg(beta) = 0.387 = Sun-Mercury
gama   = 90,456861°
              ————————
            180,0000000°

Nézzük meg a szemek fölötti két krátert fig.2. képen. Úgy tûnik, hogy meteor becsapódás hozta létre, mert egy sik területen van és egy ívsánc veszi körül. Olyan mintha a kráterbe befutó két vonal azt mutatná, itt ív van és szöget kell mérni. A szögeket mi is ívvel jelöljük. A piros háromszög csúcsa - a Feszenkov kráter - északi oldala mintha szándékkal lenne "eldózerozva", igy csak az alsó ív rajzolódik ki, és pontosan úgy ahogyan  szöget kell mérni és ábrázolni.

Ez nem egy kimagasló hegy, vagy dóm, hanem egy sík terület körülvéve egy ívalakú sánccal. Pontosan olyan ábrázolás, amelyet az iskolában tanultunk a szögek ábrázolásakor. Itt találjuk meg a csillagászati és egyéb adatok másodszori és harmadszori ismétlését. És amint láthatjuk az ismétlés mindig más-más formában történik. Az 1, 1,524, 0.387, 702 számokkal már találkoztunk a második részben, mint távolsággal megadott adatok. Itt, most megismétlik, de szögek tangenseivel. Szinte hihetelen. Azt bizonyítandó, hogy mindez nem véletlen egybeesés, az egyes háromszögek (piros, és kék), mind a három szöge hordoz információt, és pontosan adja a 180°-os összeget is.

A tang-ang nyelv használata esetén így kell feltenni az ellenörzõ kérdést: mey szög az amelynek tangense pontosan 1+1,524=2,524 ? A válasz 68,386702°, mert tangens(68,387702°)=2,524.
Ez a tangens nyelv. Ez mindenki által ismert, de nem így használtuk.

A kék háromszög másik szöge 21,156437°, melynek tangense: Tg(21,156437°)=0,387, vagyis a Nap-Merkúr közepes távolsága.
De a harmadik szög ezzel már adott.. Majdnem 90°. Méréssel természetesen 90°-ot látnánk, de a számítások adják a pontos értékeket.

Most láthatjuk azt a végtelen ötletességet, amellyel egy szöggel sokféle adatot adtak meg. Nézzük csak a szöget mégegyszer:

Tg(68,386702°)=2.524. Tagoljuk a számokat.  386 702    1   1,524
 
 - Nap - Föld csillagászati egység ........................................(1.00 AU),
 - Nap - Mars közepes távolság  ..........................................(1.524 AU),
 - Nap - Merkúr közepes távolság ........................................(0.387 AU),
 - A csillagászati egység kicsinyített mása a Marson.......     (0.007026).

Szinte hihetelen. Úgy tûnik valamire tanítani akarnak bennünket. Úgy, ahogyan Frendethal is tanitani akarta az ABC-t az ûrbéliekkel.

Mivel szögtartó térképen (Mercator-féle térkép) mértünk, a távolságok nem valósak, de a szögek igen.
De nézzük a már látot nagy vulkánok szögrendszerét. Itt is használták a "Tang-Lang" nyelvet.
 

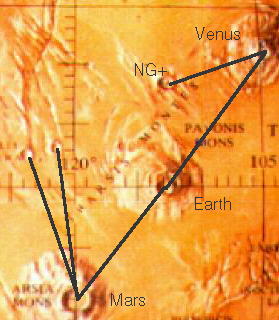
Fig. 4

.
Baloldali képen két kis krátert láthatunk. A kutatások szerint ezek csak sekély tengeben keletkezhettek. Vagy másként.
A Mars és a Föld vulkán között két kisebb, kerek bemélyedésû vulkánt találunk. Két egyenes fut b a kráter széléhez. Nézzük elõször a szögeiket.
Elõször a Föld vulkánhoz közelebbi, jobboldali vulkánt vizsgáljuk. A mérés pontosan 45°-ot mutat. A kék vonalakkal jelölt szög. Ennek tangense:Tg(45°)=1. Tehát 1. Fogadjuk el ezt a Nap-Föld csillagászati egységnek. Ez nem meglepõ, mert ennyinek kell lennie.
A másik szög (piros szög) 56,728°. Ezt a szöget nem tudjuk ilyen pontossággal megmérni, de tudjuk mrnnyinek kell lennie. A zöld, kék, piros egyenesek hossza egyenlõ és pontosan 702,6 km, hiszen körzõvel mértük ki.

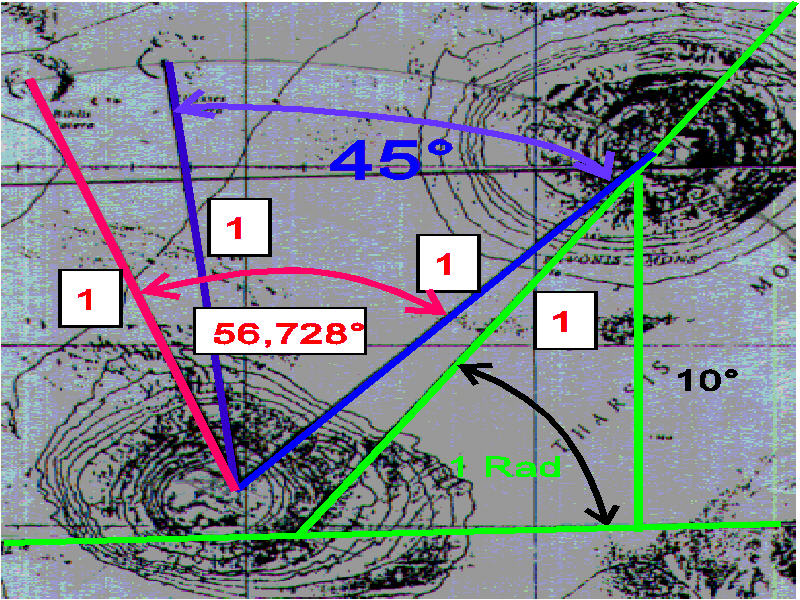Nézzük  hát hogyan alkalmazták a Tang-Lang nyelvet: 
Tg(45°)=1 és a Nap-Föld csillagászati egység is 2.

Tg(56.729)=1.524
Ez a Nap-Mars pontos csillagászati távolsága.(Piros szög)

Most, tehát újabb módon látjuk a közepes csillagászati távolságok számait.

Semmi kétség mindez akarattal így készült, és eloszlat minden kétségünket.
A két kis kráter egyenlõ távolságra van a nagy Mars krátertõl.  Mondhatjuk azt is a két kis kráter az adatai révén össze van kapcsolva.

Ha átgondoljuk, azt kell látnunk, hogy a baloldali, hosszú,  Nap-Mars egyenes oldalánál, immár másodszor van feltüntetve a két élõ bolygó, a Föld és a Mars. A második részben taglatuk, hogy a radián egyenes hogyan osztotta fel az 1773,6 km-es egyenest. 1773,6km / 702,6km =1+1,524
(De az elõzõ rajzon zöld vonalakkal ábrázolt háromszöbõl kiszámítható a 702,6 km-es távolság).
Most ugyanitt szögekkel adták meg ugyanezt az 1 és 1,524-es számot, melyet a tangens szögfüggvény ad meg.
De nézzünk a felsõ - Vénusz - vulkánt. Tõle balra találunk egy kis vulkánt melyet a NASA NG+ objektumnak nevezett el.
Megint csillagászati adatokat találunk, pontosan ott, ahol kell. (Lásd a következõ rajzot).
A Venus és Föld vulkán között a távolság 798,12 km. Most mérjük meg az NG+ objektum és a Vénusz vulkán távolságát:523,7 km.
Ha már megmértük, osztjuk el a két adatot: 798,12 / 523,7 = 1,524. Megint megkaptuk a bûvös Nap-Mars közepes csillagászati távolságot.
Ez már a negyedik alkalom, hogy bemutatták a Nap-Föld és a Nap-Mars csillagászati távolságokat.

 És most nézzünk szét a szögek között.
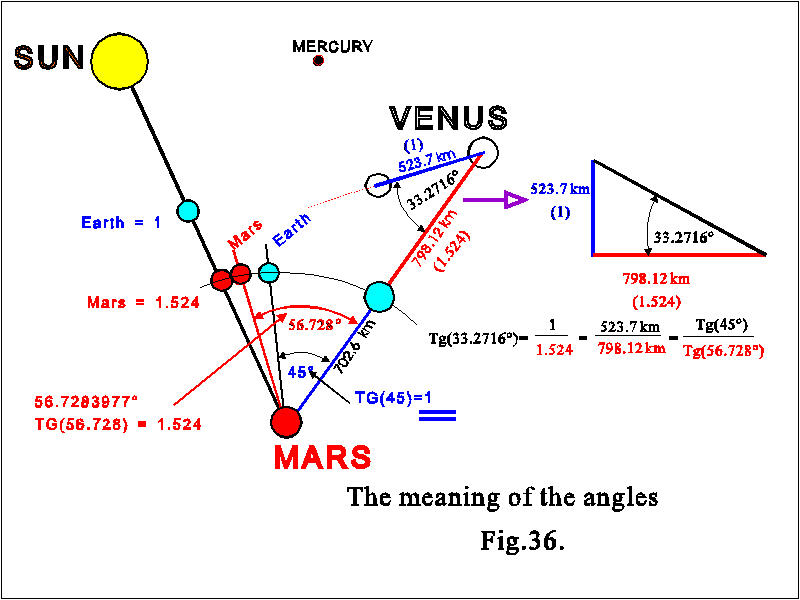Ha megmérjük az NG+ objektum szögét, akkor azt 33,.. körülinek mérhetjük. A pontos értéket szémolni lehet. Éa ekkor elámulunk. Az elõbb megadott 45°-os és a 56,728°-os szögek tangenseit osztva pontosan a most mért 33,2716°-os szöget kapjuk.
Ez így néz ki: Tg(33,2716) = 1 / 1,524 = 523,7 km / 798,12 km = Tg(45°) / Tg(56,728°)
Ezt már földi emberi ésszel nem lehet kitalálni.
 

All rigths by Attila Foldes